線形計画法のテスト問題(netlib)を読み込んで解いてみる
背景と概要
去年くらいからLPソルバを自分で書いてみたりしているのだけど、性能を評価するためのテストケースをどうしようかと思ってWeb検索したりAIに相談したりを何度も繰り返して結局どうしてよいかわからないという状況が続いている。どこかで公開されていたらそれを使うのがベストなのだと思うけど…😖
— Ozy (@ozy4dm) 2023年7月3日
線形計画法のテスト問題が欲しいー!とつぶやいたところ、
まずは古くから使われていて小規模な問題が多い netlib がおすすめです.(ダウンロードは面倒)https://t.co/nPH32zGEHA
— 今井義弥 (@imai_yoshiya) 2023年7月3日
Mittelmann 先生が公開しているのは,netlib などの様々なデータセットから比較的難しい問題を選んだものかと思います.https://t.co/YaIjw4sUaN
と、具体的に教えていただいたので、実際にデータを入手してPuLPを用いて解いてみました。MPSファイルを生成するのに少し手間がかかるので、メモ的に書き残しておきたいと思います。
問題データを手に入れる
データはhttps://www.netlib.org/lp/data/からダウンロードできます。 ただ、データフォーマットが圧縮MPSになっているのでまずこれをMPSファイルに展開する必要があります。
empsというプログラムが必要なので、まずこれを生成します。FortranとCのコードがありますが、私はCの方を使いました。
curl -L -O http://netlib.org/lp/data/emps.c
で入手して、
gcc -o emps emps.c
みたいな感じでコンパイルしてください。実行ファイルができたら、
emps < 圧縮MPSファイル名 > MPSファイル名
という感じで使います。試しにページの一番上にある25fv47というデータを使ってみます。
emps < 25fv47 > 25fv47.mps
みたいにすればOKです。
PuLPで解いてみる
次にこのデータを適当なソルバで解いてみることにします。 今回はPuLPで解いてみました。Pythonがすでに使えるものとして、
pip install pulp
でPuLPを使えるようにしておきます。コードは以下の通りです。第一引数にmpsファイルのパスを取るようにしておきます。
import sys import pulp mps_file_path = sys.argv[1] variables, problem = pulp.LpProblem.fromMPS(mps_file_path) problem.solve()
たったこれだけ。超簡単ですね!実際に動かしてみると、次のような出力が得られました。
... 最初の方は省略 ... Optimal - objective value 5501.8459 After Postsolve, objective 5501.8459, infeasibilities - dual 0 (0), primal 0 (0) Optimal objective 5501.845888 - 1718 iterations time 0.152, Presolve 0.01 Option for printingOptions changed from normal to all Total time (CPU seconds): 0.17 (Wallclock seconds): 0.20
問題データのダウンロード元にあるhttps://www.netlib.org/lp/data/readme:readmeを見ると、次のように書かれていました。
Name Rows Cols Nonzeros Bytes BR Optimal Value 25FV47 822 1571 11127 70477 5.5018458883E+03
ちゃんと解が得られたようです。やったー!
というわけで、この情報を教えてくださったimai_yoshiyaさんと、最初にアドバイスをくださったオノウェイ先生に感謝!!
今後自分のソルバで何か成果が出たら改めてきちんと記事にしたいと思います。
追記
結構面倒だったので、まとめて処理しておきました。 https://github.com/ozy4dm/lp-data-netlib
しかし以下の問題について、データの生成ができていません。
- QAP8
- QAP12
- QAP15
- STOCFOR3
QAP8, QAP12, QAP15については、こちらからジェネレータを手に入れる必要があります。
また、STOCFOR3については実行時にエラーが発生します。トライしてみた結果、以下のようなエラーメッセージが表示されました。
% ./std2mps
Process TIME file:
1 TIME STOCHFOR
10 ENDATA
Process CORE file:
1 0.0000 0.0000
XXX - FATAL - Illegal record in CORE file
STD2MPS: execution terminated.
解決したら更新しておこうと思いますが、今のところよくわからないのでそのままにしておきます。
競プロ日記013: 日立北大コンの表彰式&意見交換会
表彰式&意見交換会に行ってきました
Hitachi Hokudai Lab. & Hokkaido University Contest 2022(日立北大コン)のB問題の成績で(ギリギリ)お呼ばれして、参加することができました。
経緯
意見交換会で発表しませんか?
オンラインで視聴できるかなーという程度で考えていたのですが、2月27日になって「意見交換会ご講演依頼」というメールが届きました。表彰式と意見交換会の3月3日まで結構日が迫っている中でのメールということで、「もしかして人がいなくて人数合わせ的な!?」と思ったりもしましたが、せっかくなので発表の機会をいただくことにしました。
最後とか罰ゲームじゃね?
YESの返事をして、大急ぎでスライドを作ってる最中に当日のスケージュールが来たのですが、発表の順番が成績順だったのですよ。上の方が優れているに決まっているし、特にB問題の発表者は1, 2, 3, 4, 6位とトップクラスの人しかいないので、自分の順番が回ってきた時点でもう話せることないんじゃないかと思って10分中8分くらい自己紹介したろかなと考えたりもしてたのですが、結果的にやらなくて良かったです(後述)。
当日
初手・遅刻
いきなりやらかしまして、12時30分までの表彰式を12時30分からだと思い込んで行った結果、大遅刻しました。終了10分くらい前に、こそこそっと入室して最後尾から見ていたのですが、眼が悪すぎてあまり見えないし動揺して話も全然入ってこないしでホント情けない状態でしたが、声を書けてくださった方が少しいたおかげで落ち着きを取り戻すことができました。
バス移動・お昼ご飯
表彰式が終わったらマイクロバスで別の場所(地理は全くわかっていない)に移動ということで、言われるがまま乗り込みました。作問者の方と少しお話しすることができました。なんと私のことをご存じだったとのこと!どうやら昔書いていたショートコーディング関係のブログをご覧いただいていたようで…。何でもやってみるものですね😅
会場についてから、美味しいお弁当をいただきました。
意見交換会
上位の方々の発表を「なるほどなー」と思いながらボケっと聞きながら、少しずつ「あれ?」と思いはじめました。みんなオンライン参加なんですよね。じゃあ自分の周りにいる人々はどちらさま???
終わって確認してようやく気が付きましたが、自分以外は出題側の方々でした…。「あっ、あなたがid〇〇さんなんですね!どうもはじめまして!!」というのを想像しながら参加していたので、これは衝撃でした。と同時に、最初「自己紹介8分ぐらいやろかな」とか思っていた自分を思い出して、とても申し訳ない気持ちになりました。できるだけ真面目モードに軌道修正したつもりですが、ホントすみませんという感じです。
内容的なお話と感想
意見交換会では、基本的には問題内容やこれまでのコンテストをよくご存じのsimanさんが、発表者の方々に重要なポイントを質問なさっていて、私はふんふんなるほどしていただけなのでとてもありがたいお話を賜っただけでした。
コンテスト中考えもしなかったのですが、今回の問題って受託必須ジョブなのに完了できないものがあったのですね。自分の解答はあきらかに最適化性能が低い自覚があったので、未完であっても「まあしかたないよね」としか思っていませんでした。
他の方々にとってはあまり役に立たなかったような気がしていますが、自分にとって結構大きな収穫がありました。simanさんが天気予測に関する質問をたくさんなさっていて、自分もそれがとても気にはなっていたんですが、上位の方々は最終的に何か特別なことをするというよりもシンプルな期待値を設定しているだけのようで、ここは自分の想像と大きく異なりました。
帰宅してから上位陣のコードを読んだり動かしたりちょっといじってみたりして確認してみたところ、自分がコンテスト中に思いついた調整を試してみてもほとんど効果が無いんですよね。最上位のレベルになると、そもそも探索性能が高くてよくわからないパラメータをどうこうするより単純に高速化とかしてた方がずっと効果的であるようでした。
思い返せば自分が今まで参加したマラソンマッチでも、「雰囲気パラメータ」を作って何となくいじって何となくスコアは上がるものの、上位からは程遠い結果に終わるケースが多々ありました。
つまり何となくコードを変更してみて何となくスコアが上がっている状況というのは、やってる感は多少あるものの根本的な問題から遠いところで何かやっているに過ぎないということです。これは自分にとって大きな収穫だったと思います。
とにかくレベルアップを
今回は現地に行って、参加者でない人々に補足的な説明をしたり多少の賑やかしには貢献できたような気もしますが、やっぱりもっと問題そのものに対する議論に参加できるレベルになっていたかったというのが正直なところです。最近は参加しっぱなしで復習もまとめの記事も書けていないことが多いので、ちょっとなんとかしないとという気持ちはより強くなりました(と言いつつコンテストの予定が発表されるとすぐに飛びついてしまいますが…)。
しばらくは何でも積極的にやるしかなさそうです。

ショートコーディング完結編
はじめに
ショートコーディングという本を書いてから、16年近く経ちました。当時のスキルを思えば120%の力で書ききったものではありましたが、ずっと心残りだったことがあります。
それはCのマクロについてです。マクロを使ってより短いコードを書くことができるのではないかと思いつつも適当な問題が見つからず、また自分で作ることもできず、「今のところできないけどできるかもしれない。」という結論にせざるを得なかったわけです。
しばらくはそのことも記憶の隅に追いやっていたのですが、年に1回くらいは思い出してしまい、Anarchy Golf(あなごる)のCの記録を覗いてみるということを繰り返していました。そして2016年、すばらしい作品に出合いました。
…とまあ、感想文を書いていても仕方ないので、そういうのは最後に書くこととして、ショートコーディング本の最後のピースとして、マクロを利用した超記録とその解説をしたいと思います。紹介する問題は「Fractal X」というフラクタルのAAを出力する問題と「Big Fibonacci Number」という大きなフィボナッチ数を計算する問題の2つです。
この2つの解は、いずれもゴルフ神のtailsさんによるもので、ここでの紹介・解説することにも快く応じてくださいました。心より感謝いたします。 なお、本ブログは私Ozyが勝手に書いたものですので、内容に誤りがあったとしても私が間違えたものであり100%私の責任です。ご了承ください(もし誤りがあった場合はご指摘いただけるとありがたいです)。
では始めましょう!
Fractal X
問題概要
このFractal Xという問題は、入力なしで次のようなAAを出力するコードを書くというものです。

基本的な考え方
まずは小さなX
X X X X X
を作ってみたいと思います。
#include<stdio.h> void f(int x) { if(x >= 4) { printf("%d ", x); } else { f(x * 2); // X_X f(x * 2 + 1); // _X_ f(x * 2); // X_X } if(x / 2 == 1) puts(""); } int main(int x) { f(1); return 0; }
これを実行すると、次のような出力が得られます。
4 5 4 6 7 6 4 5 4
フラクタルの問題なので、再帰的な関数呼び出しがよくマッチしていますね。再帰関数内で3回再帰することで、AAの縦横サイズを3n倍にすることができます。
上記の4と7の部分をXにしたいので、出力部分を次のように書きます。
printf(x % 3 == 1 ? "X" : " ");
これで小さなXを作ることができました。次はこれを拡大していきます。
void f(int x) { if(x >= 16) { // ←ココ! printf(x % 5 == 1 ? "X" : " "); // ←ココ! } else { f(x * 2); f(x * 2 + 1); f(x * 2); } if(x / 4 == 1) puts(""); // ←ココ! }
こんな感じでひと回り大きなXができました。
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
こんな感じで必要な大きさまにまで育ててやったものが次のコードです。
void f(int x) { if(x >= 256) { printf(x % 17 == 1 ? "X" : " "); } else { f(x * 2); f(x * 2 + 1); f(x * 2); } if(x / 16 == 1) puts(""); }
main再帰と基本短縮
この問題では入力の心配をする必要がありませんので、main関数自体を再帰することも難しくありません。
int main(int x) { if(x >> 8 != 0) { // x >= 256 if(x % 17 == 1) putchar('X'); else putchar(' '); } else { x *= 2; main(x); main(x + 1); main(x); } if(x / 32 == 1) puts(""); }
引数なしの実行ではmain関数の第1引数が1になることも利用すれば、非常にスッキリとしたコードになります。これを基本通りに短縮してやると、次のようになります。空白文字や改行を取り除くと82バイトと、かなり短いコードになりました。
main(x){ x>>8?putchar(x%17-1?32:88):main(x*=2)+main(x+1)+main(x);x/32-1||puts(""); }
マクロの出番が来た!
「main(x」という記述が4回も現れました。文字数にして24文字です。これをマクロで置換すると、以下のようになります。
#define m main(x m){x>>8?putchar(x%17-1?32:88):m*=2)+m+1)+m);x/32-1||puts("");}
一見コンパイルすら通らなさそうな見た目ですが、ちゃんとコンパイルできます。そして先のコードより3バイト短い79バイトのコードになりました。
マクロを使うと、#define ...の部分がそれなりの文字数になるため利用できるケースが少ないですが、このように数多く繰り返すケースであれば利用できることが確認されました。
では次に、大きなフィボナッチ数の問題について解説していきます。
Big Fibonacci Number
問題概要
Big Fibonacci Numberでは、大きなフィボナッチ数を出力します。
フィボナッチ数列を、
n > 2のとき
と定義します。
このときnが入力として与えられるので、f(n) mod 1000000000(1e9)を出力するという問題です。
なお、入力の最大値は1000000000(1e9)となっています。
Cにはきつい問題
Cにおけるゴルフの基本的なテクニックとして、
型名を省略→(32bit)int型として扱う
というものがあります。しかしこの問題では扱う値が大きいので、少なくとも(long longのような)64bit整数が欲しいところです。また、入力も大きめですので愚直に計算すると制限時間内に解答することができません。
つまり、ポイントとして次の3点を考慮する必要があります。
- 大きな整数値を扱う
- 計算速度も必要
- 最短コードを狙う
基本的なアイデア
変数について
long longのような記述は基本的に避けたいので、64bit整数型の変数は使いません。幸い出力はmod 1e9で構わないので、うまくやれば32bit整数型の変数だけで何とかできるはずです。
計算方法について
フィボナッチ数を高速に計算する方法で一般的なものとして、
のように行列を使う方法があります。
しかしこれをCでそのまま実装すると、次のように結構なコード量になります。
#include<stdio.h> #include<string.h> #define ll long long #define M 1000000000 ll p[30][4] = {{1, 1, 1, 0}}; void mul(ll *a,ll *x,ll *y) { ll t[4]; t[0] = (x[0] * y[0] + x[1] * y[2]) % M; t[1] = (x[0] * y[1] + x[1] * y[3]) % M; t[2] = (x[2] * y[0] + x[3] * y[2]) % M; t[3] = (x[2] * y[1] + x[3] * y[3]) % M; memcpy(a,t,sizeof(t)); } int main() { int n; for(int i = 1; i < 30; ++i) { mul(p[i], p[i - 1], p[i - 1]); } for(;~scanf("%d",&n);) { ll k[4] = {1, 0, 0, 1}; for(int i = 0; i < 30; ++i) { if((n + 1) & (1 << i)) mul(k, k, p[i]); } printf("%lld\n", k[1]); } return 0; }
他に高速化する方法としてよく使われる方法は配列を使ったDPやメモ化再帰で、実用上は問題ないことが多いのですが、この問題の場合は入力の最大値が1000000000です。4バイト整数の配列を用意するとなると、4GB近く必要になりますので、ちょっとしんどいですね。
周期性を利用できるか
フィボナッチ数列の周期性を利用できるかもしれませんので、調べてみました。
| 桁数 | 周期 |
|---|---|
| 下1桁 | 60 |
| 下2桁 | 300 |
| 下3桁 | 1500 |
| 下4桁 | 15000 |
| 下5桁 | 150000 |
| 下6桁 | 1500000 |
| 下7桁 | 15000000 |
| 下8桁 | 150000000 |
| 下9桁 | 1500000000 |
桁数が増えると周期はかなり長くなるため、出力サイズが9桁の場合は必要な配列サイズを超えてしまっていて利用するのは難しそうです。
この時点で行列を使った方法をベースに気合で短縮していきたい気分になるところですが、本物は違いました。
最短コードに向けて
まず計算量を落とす
フィボナッチ数列には、
が成立するという面白い性質があります。証明・解説は省略しますので、参考として高校数学の美しい物語 > フィボナッチ数列の7つの性質(一般項・黄金比・互いに素)をご覧ください。
この式において、m = nとすると
となり、m = n + 1とすると
となります。
つまり、入力が偶数の場合と奇数の場合で計算方法が少し異なりますが、同じような式の形で計算できそうです。 またこの方法を使うとfの呼び出し毎に引数の値が約1/2倍になり、定義通りの漸化式と比べて計算量が格段に少なくなります。メモ化なしのコードは次のようになります。
#include<stdio.h> #define ll long long #define M 1000000000 ll fib(ll n) { if(n <= 2) return 1; int m = n / 2; // nが奇数の場合は小数点以下を切り捨てる if(n & 1) { return (fib(m) * fib(m) + fib(m + 1) * fib(m + 1)) % M; } else { return (fib(m - 1) * fib(m) + fib(m) * fib(m + 1)) % M; } } int main() { int n; for(;~scanf("%d",&n);) { ll ans = fib(n + 1); printf("%lld\n", ans); } }
これで入力が5桁くらいまで動くようになります(定義通りだと2桁程度が限度です)。かなり高速になりましたが、より大きな入力にはメモ化せざるを得ません。
消費メモリを少なくする
先のアルゴリズムでは、関数の呼び出し回数を大幅に少なくする効果がありましたがそれはメモ化回数も少なくしているということになります。入力が最大(1000000000)の場合でも、実際に配列に書き込まれる値は100個程度しかありません。C++であればmapを使ってかなりコンパクトに書くことができます。Cではmapが使えないため、小さめの配列にマッピングすることで実現可能です。
#include<stdio.h> #define ll long long #define M 1000000000 #define W 99999 ll memo[W]; ll fib(ll n) { if(n <= 2) return 1; int w = n % W; if(memo[w] > 0) return memo[w]; int m = n / 2; // nが奇数の場合は小数点以下を切り捨てる if(n & 1) { memo[w] = (fib(m) * fib(m) + fib(m + 1) * fib(m + 1)) % M; return memo[w]; } else { memo[w] = (fib(m - 1) * fib(m) + fib(m) * fib(m + 1)) % M; return memo[w]; } } int main() { int i, n; for(;~scanf("%d",&n);) { for(i = 0; i < W; ++i) memo[i] = 0; ll ans = fib(n + 1); printf("%lld\n",ans); } }
ハッシュ計算が雑過ぎるので競プロ的にはアウトだと思いますが、すべての入力がわかっているあなごるでは衝突の心配をあまりする必要はありません。もし衝突したら配列サイズや計算方法を変えれば良いですからね。
これで基本的な準備は終わりました。
偶奇の分岐を無くす
小数点以下の切り捨てを上手く利用すれば、偶奇による分岐を無くして1行で書くことができます。
ll fib(ll n) { if(n <= 2) return 1; int w = n % W; if(memo[w] > 0) return memo[w]; memo[w] = (fib((n - 1) / 2) * fib(n / 2) + fib((n + 1) / 2) * fib((n + 2) / 2)) % M; return memo[w]; }
計算結果は32ビット整数に収まることがわかっていますので、そろそろint型のみの変数を使ったものに書き替えて、コード全体を手直しします。
#include<stdio.h> #define M 1000000000 #define W 99999 int z[W],i; int f(int n) { if(n < 5) return 1; int w = n % W; z[w] = z[w] ? z[w] : (1LL * f((n + 1) / 2) * f((n + 2) / 2) + 1LL * f((n + 3) / 2) * f((n + 4) / 2)) % M; return z[w]; } int main(int a) { for(;~scanf("%d",&a);) printf("%d\n",f(a + 3)); }
計算途中で32ビットを超えてしまいますので、関数fの戻り値に1LLをかけてlong long型に変換しておきます。あとはここから基本的なテクニックや基本的じゃないテクニックを駆使してコードを短縮していくのですが、かなり複雑になりますので詳細は省いておきます。興味のある方は手元でやってみて、動くかな?と思ったらあなごるのCheckerで動作確認してみてください。
マクロを活用する
関数呼び出しの部分と、64ビット型にキャストする部分がどうしても冗長になってしまいますが、ここでマクロを利用します。
#include<stdio.h> #define M 1000000000 #define W 99999 #define F 1LL * f(++n / 2) int z[W],i; int f(int n) { if(n < 5) return 1; int w = n % W; z[w] = z[w] ? z[w] : (F * F + F * F) % M; return z[w]; } int main(int a) { for(;~scanf("%d",&a);) printf("%d\n",f(a + 3)); }
す、すばらしい…。
至高の129B
#define F 1ll*f(++n/2) m=1e9;h[5686];i;f(n){h[i=n%5686]=h[i]|n<5?:(F*F+F*F)%m;}main(){for(;gets(&i);printf("%d\n",f(atoi()+3)));}
getsの部分はhに読み込むことで1B減らすことができるみたいですが、あえてtailsさんのコードをそのまま掲載します。
- 高速
- 省メモリ
- 処理系依存
- テストケース依存
全てが調和した上で仕上げのマクロという、私が夢見ていたコードにやっと出会ったと思いました。本当にすばらしいです。
ショートコーディング完結編
ここから感想文です。
コードゴルフの認知度って結構上がりましたよね。いろんなところで目にするようになりました。ショートコーディング本に書かれていない変態的テクニックもいろいろと存在しています。私はというと、あなごるは定期的に観察しているものの提出まで至っておらず、年に一回程度POJで遊ぶくらいです。ご存じの方もいらっしゃるかもしれませんが、最近はマラソンマッチにお熱です。
そんな私でも、今回紹介した大きなフィボナッチ数の問題だけはいつも頭の中にありました。もしショートコーディング本を書いている頃にこの問題に出会っていたとしても、マクロを使ったコードはまったく思いつかなかったと思います。いつ見ても、何度見ても素晴らしい。今日もこのコードを観ながらご飯食べてます。
無知が原動力
アルゴリズム・データ構造・処理系等々、知らないことが多すぎて、何を見ても何を聞いても何をやっても、すべてが新鮮で本当に面白い。そんな状況でショートコーディング本を書いていました。そもそもショートコーディングなんてワードはコードゴルフというものを良く知らないが故に産まれたようなものですからね。
さて、今はと言いますと、当時と比べてそれなりに知識も技術もある程度レベルアップしました。もちろんまだまだ知らないことはあるのですが、新しいモノを生み出すモチベーションになるのかというとそれは少し微妙です。むしろコードゴルフを最近知って「面白い!」と感じた若い人がたくさん発信した方が、絶対良いと感じています。
記事も本も書かないのか
書かないということはたぶんなくて「Cゴルフ」みたいなもうちょっとコンパクトでお気持ち少なめの何かとか、シェル系のゴルフには興味があります。何よりPOJで遊ぶのは私の楽しみのひとつですので、ときどき何かやりたいなーと思っています。
本当に完結なのか
完結しない可能性が1つあります。今回紹介した2つのコード以外でもhttp://golf.shinh.org/reveal.rb?Fire+Emblem+4+RNG/tails_1551928236&cのようにマクロで最短を取っているものがあるのですが、これらの記録がすべてマクロを使わないコードに破られてしまった場合、「やっぱマクロ意味ないじゃん!」と言われてしまう可能性があります。その時はまたマクロの可能性について考える旅が始まるかもしれません(お願いだから始まらないで欲しい)。
というわけで
ここまで読んでくださった方はありがとうございました。どうしても今日投稿したい、今日しなかったら一生しないと思い、超特急で書きあげました。記述に雑な部分はいろいろとありますので、後日修正したいと思います。何か問題点等あればご指摘いただけると嬉しいです。ではまた!
おまけ
毎年2月11日は、ゆるっとPOJで遊んでいます。今年は3970番をやっていました。そしてまたushiodaさんに負けました…くやちいぃ!


競プロ日記012: AHC017の解法解説
AHC017 最終50位(暫定49位: 40.3G / 50.0G)の解法
THIRDプログラミングコンテスト2022(AHC017)の解法と,約一週間のコンテスト期間のアプローチについて解説(というか記録)しておきます.ヒューリスティック系コンテストの初心者・中級者や未来の自分の役に少しでも役立てばと思います.
問題の概要
N地点と,各地点を結ぶM個の道があります.この道のいくつかを補修工事するのに通行止めする必要がありますが,そうなると移動が不便になり,不満度が上がります.不満度はある地点から他の地点を移動する際の移動距離が増えるほど大きくなります.工事を行う日数Dと,一日に工事できる(通行止めできる)道の数の上限Kが与えられるので,これらの制約の中で可能な限り不満度を小さくするような工事計画を立てるという問題でした.
最初と2番目のアプローチ
まず最初にやったことは,1 1 1 ... 2 2 2 ... 3 3 3 ...のように適当に出力するコードの提出です.一度提出しておくと実際のスコアが得られるので,それを基準にローカルでのテスト環境を作ります.これをしておくと何度も提出してスコアの確認をする必要がなくなるので,基本的にやっておいた方が良いと思います.単にスコアボードを見て,似たような解答だろうなーという人のスコアを参考にするのも良いのですが,今回は同じ得点が何パターンかあったので,より正確に把握するために提出しました.
次にやったことはテスタの自作です.通常は付属のテスタをそのまま使うのですが,スコア計算の速度が遅すぎてストレスになることが目に見えていたからです.どうせ自分の解答プログラムを作るときにスコア計算を実装しなければならないですから,ここで慌てずある程度高速で正確にスコアが出せるように実装しました.高速とは言っても,まずは特別なことをせず愚直に実装します.
公式のテスタと同じスコアが出力できるようになったことを確認したらひとまずヨシとします.この時点では公式テスタと大して速度差はありませんが,問題本体のアイデアに詰まったときに気分転換として高速化をしていこうと決めました.
今回の自分ルール
本格的にマラソンマッチを始めて1年近く経ち,なんとなく心構えのようなものができてきたということもあり,今年は安定して結果を残すということを基本的な目標にしています.途中でくじけないように,簡単なルールを決めました.
- スコアが満点に対して7割程度になるまでは貪欲解法を中心に
- 高速化は煮詰まったときの気分転換としてやる作業とする
- 直感に反することでも必ず試す
- 最後まで諦めない
最初のアイデア
最初の時点でスコア計算に1秒近くかかっている状態だったので,まずは少ない計算量で良い計画/悪い計画を調べる必要がありました.いきなり躓いたので速い気分転換ということで,あまり頭を使わない高速化(2次元配列を1次元にとか)をちまちまと行いながら,「とりあえず到達不能な経路を作らないようにしよう」ということだけ目指すようにしました.
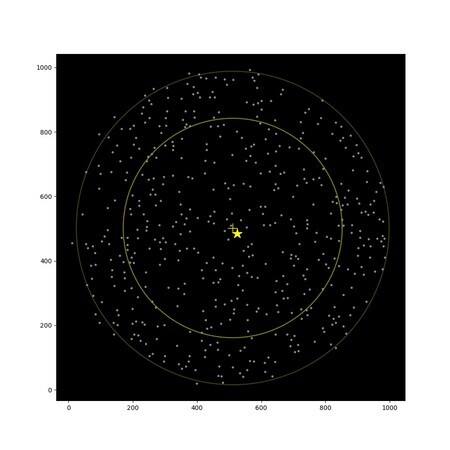
そう考えると割と簡単な話で,どこか1地点にだけ着目すればよいことになります.1地点からそれ以外の点に全て到達可能なら,他の点は調べなくてもちゃんと到達可能だとわかるからです.ではどんな点を選ぶべきかと考えました.少なくとも最初に1回,全ての点からの最短経路を求めているので,ついでに各点までの距離の合計も計算しておくことにしました.そして,距離の合計が最も小さい地点はおそらく盤面上の重心近くだろうという結論に至りました.
次の図はseed386を使って,この記事のために作成したものです.+は全ての点の重心で,★はその地点から他の点への最短距離合計が最も小さくなる点です.思った通り重心近くになっていました.
この考え方を元に,最初の解答プログラムを作成しました.Dが小さい(5とか)の場合に上手くいかないこともありましたが,あまり気にせずに100ケース程実行してみます.そうすると,最初の解より2~3倍スコアが良くなったので,この方針で大丈夫だろうと判断しました.提出すると,26G程度のスコアが出ましたが,実行時間は4秒くらいかかっていました.
いきなり詰まる
最初の解法ですでに4秒も消費しているのと,正直ノーアイデアに近かったので,早速高速化タイムに突入しました.方針としては,
- この数日で次のアイデアが何か出るだろう
- もしそれが上手くいけば,次のステップ(おそらく山登り)に進める
- いろいろ準備をしておこう
です.つまり,高速化をして初期解を得るまでの時間を短くし,後半の山登り(道を入れ替えてスコア算出を繰り返す)をできるだけたくさんできるようにしておこうと考えました.とはいえこの時点では差分計算まで考えていなくて,小手先の高速化(queueをやめて固定長配列を使う等のチマチマしたもの)で,初期解を2秒くらいで得られるようにしました.さらに入れ替え山登りフェーズも追加して動かしてみると,到達できない点が現れるケースが無くなり,この時点で推定30G程度のスコアになりました.推定というのは,実際に提出せずにスコアボードの状況と自分のローカルテスト環境の結果を比較して算出したということです.
観測地点を複数にしたい
この辺りから実行時間を延長してみるということを試しました.スコアが上がれば単に高速化すればよいことがわかります.実際にやってみると,確かにスコアは上がりましたが少し物足りません.要するに,1点からの距離だけで考えると改善の見込みが無くなってしまうからです.そこで,今後も何らかの高速化によって実行時間を確保するという前提で基準にする点を増やしてみることにしました.ランダムな点も悪くはなかったですが,最終的に重心から同心円状に配置することにしました.次の図は3点を置いた場合と5点置いた場合です.重心からの距離は,半径の70%としました.
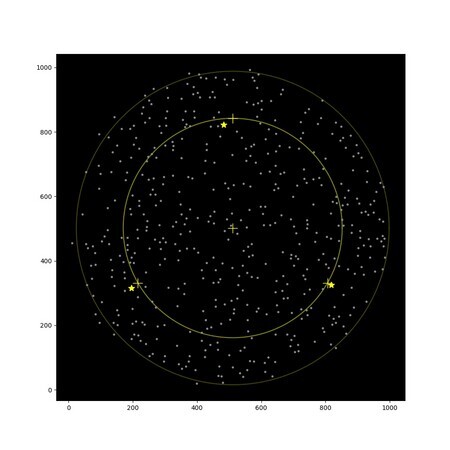
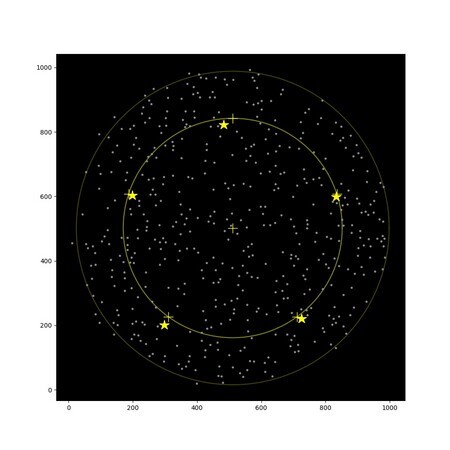
5つ置いた場合が最もスコアが良くなりましたが,制限時間の6秒では収まらなくなってしまいました.
苦し紛れの噓ヒープ - Liekstra's algorithm
本来ならここできちんと経路復元して差分計算を行うべきだったのですが,「早く完成品を仕上げたい」という誘惑にまけて小手先の高速化に徹してしまいました.今振り返って,失敗したと感じたのはこの点ですが,それなりに高速化されたので一応記録として残しておきます.通常のダイクストラ法はpriority_queueを使いますが,私は最初から普通のqueueを使っていました.普通のqueueだとNが大きいときに遅くなってしまうため,取り出す点の優先度は欲しい,しかしpriority_queueは遅い…ということで,妥協案として次のような操作を行いました.
- 要素を普通にpush
- 先頭の要素と末尾の要素を比較する
- 末尾の値の方が先頭の値より小さければswap
割と単純な操作ですが,できるだけシンプルなコードにして実行回数を増やすことで強引に速度アップさせました.ちゃんと差分計算したものよりは圧倒的に遅いですが,これで何とか制限時間の6秒に収まるようになりました.この時点で推定35Gくらいです.
停滞期
噓ヒープを選択することによりアルゴリズム的な工夫をする意欲が無くなってしまい,長い停滞期に入ることになりました.細かい調整をして37~38G程度までは上がりました.順位的にも100位以内に入れそうだし,このままゴールしても良いかな…と一瞬思ったのですが,最初のルール『最後まで諦めない』に違反していると思い直して粘ることにしました.でも焼きなまし的な何かをしようとは思いませんでした.速度の問題で山を登り切れていない状態で焼きなまそうとしても無駄だからです.ここでもう一度最初のルールを思い出します.『スコアが満点に対して7割程度になるまでは貪欲解法を中心に』これに徹するべきだと思いなおしました.
初期解の改善
この時点で締め切りまで3時間程度になっていました.「まだ工夫していないことは何か?」をよく考えた結果,計画に追加する道の順番がずっとランダムな状態のままだったことに気付きました.こういうのはまばらに設置した方が大体良いと思い込んでいましたが,『直感に反することでも必ず試す』というルールに乗っ取って,地点ベースで優先度を与えることにしてみました.
- 適当に1地点選ぶ
- そこに接続しているすべて道を日程に組み込む
- すべての道が組み込まれるまで繰り返す
これで少しだけスコアが上がりました(1.5%くらい).なるほど,では地点の選び方も順序を決めて,起点(とりあえずランダム)の道を全て選んだら,その道に接続する点を次の候補としてさらに道を追加する,つまりBFS的な順序で道を追加していく方針にすると,さらにスコアが上がりました.では起点はどこか?一番最初のアイデアに戻りました.1点だけ選んだ点は,「そこから各地点までの距離の総和が最小になる点」でした.
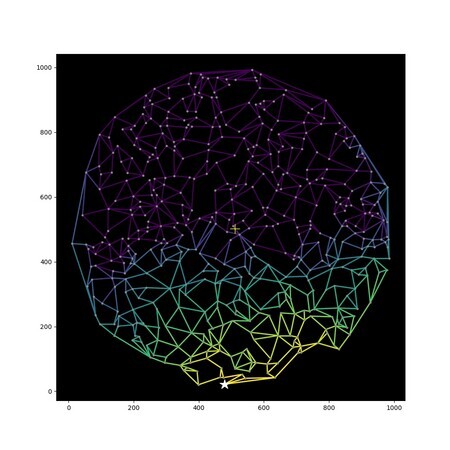
しかしスコアは上がりませんでした.良さそうなのに….しかしよく考えると,選ぶ道をかなり偏らせてスコアが上がったのだから,起点も距離の総和が最小なのではなく最大になる点を選べば良いのでは?と思いなおし,そのような点(つまり移動に最も不便な点)を起点にすると,最終的に5%くらいスコアが上がり40Gに到達しました.次の図は最終提出の解法で選んだ道の優先順位です.★が起点で,明るい(黄色い)辺を優先的に計画に組み込んでいきます.
反省と感想
やはり差分計算をサボったことが悔やまれます.後から実行時間を10倍にして1000ケーステストしたところ,スコアは8.6%程度増えました.ちゃんと高速化していればもう少し良い結果になったでしょうし,そこまでくるといよいよ焼きなましが使える段階になります.そこまで行きたかったというのが正直な感想ですが,今の自分の実力なら上出来だとも思います.とにかく安定して結果を残せるように,しばらくは今回のルールに加えて
- アルゴリズム的な高速化は優先的に行う
を基本的に守ってコンテストに参加していこうと思います.次の目標はランキング1ページ目!
競プロ日記011: 今年のまとめ
今年からマラソンマッチを本格的に始めました。また、マラソン力強化のためにAtCoderのアルゴにも挑戦してみました。来年以降もしばらく続けてみようと思うので、将来の自分とこれから競プロをやってみようかと思う方々の参考として、これまでのまとめを記録しておきます。
TopCoder Marathon Match(MM)
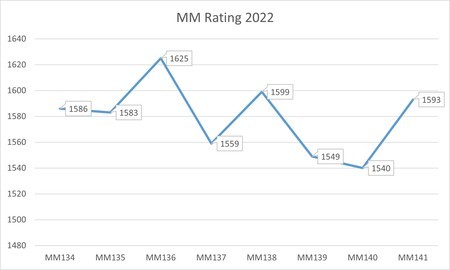
2013年に初めてマラソンマッチに参加して、この時のレーティングが1720だったので、まずはそれを目指しましたがなかなか成績が安定せず、最高でも1625でした。しばらくはギリギリYellow Coderが続きそうです。とはいえ、初参加時の何となく解法と比べると自分が何をしようとしているか理解した上で解答できている感覚はとても大きくなっているので、単純に数値で判断するのも良くないかなと感じています。
現状では問題点が割とはっきりしています。それは、「自分より上位の人とアイデアはさほど変わらないのに、常にスコアが1割くらい低い」ということです。どうしてかというと、最適化云々以前に自分の実装がゆるいからです。たとえばグリッド上で最短経路を求めるようなケースで複数の案がある場合、状況に応じてその中からより良さそうなものを見つける、あるいは優先順位がつけにくい場合に確率的な偏りの少ない案を選ぶとか、その辺りの対処がきちんとできていない場合が多かったです。
これは単なる一例ですが、あらゆる実装面でこのような緻密さが足りないことが多く、その結果探索の精度が落ちるため持ち時間の10秒を十分に活かしきれていません。今後はその辺を丁寧にやる訓練が必要です。スコアが上がらない場合にほぼ100%陥ってしまったのは、「上位の人はきっと天才的なアイデアをもっているからだ。自分のような凡人には思いつけないんだ😢」という思考になって自分の今やっていることを信じられなくなるというミスでした。この辺は自分の実績とか性格の影響が大きいと思いますが、もっとトレーニングと実戦経験を重ねて克服するしかありませんね。
AtCoderアルゴ
MMと短期AHC(AtCoderヒューリスティック)の力を鍛える一環として、短時間でのコーディング力を高めるためにアルゴの方にも何回か参加するようになりました。とりあえず今の実力だと、このまま続けると緑くらいまではいけそうかなーというとことで止まっています。マラソンに役立っているかというとあまり関係なさそうというのが現時点の感想で、どちらかというとこれはこれでちゃんと過去問とか対策をして真剣に取り組んだ方が絶対面白いような気がしています。もう少し時間にゆとりができたら、将来的にこちらも本格的にやってみたいかなという気分です。
現状では3~4問解けるくらいで順位が大体2500~3000辺りですが、同じ解答数でも解くスピードが速いと順位的には1000くらい差が出るみたいです。最初の4問を高速に解答できたと仮定して5問目を解いた場合にACできたりもしているので、基本的にはスピードアップのトレーニングをすべきですね。周囲を見渡すと1000問以上解いている方ばかりなので、来年はできるだけたくさん解いて、500問くらい解いたらABCに数回チャレンジしようと思います。
それから使用言語に結構悩んでいて、Pythonで書いてみたりC++で書いてみたりしていたのですが、当初のMMの力を鍛えるという当初の目的からぶれないようにC++一択でやろうと決心しました。まあMMのことを考えなくても、PythonでTLEしたときに「もしかしたらC++なら通るかも…」みたいな気持ちになりたくないという気分ということもありますが…。
来年に向けて
一番はやはりMMで過去の自分を超えることですね。それから、AHCの方もMMと同じくらい頑張りたいと思います。ただ、スケジュール的にAHCとMMが重なったり、AHCが短期コン(4時間)とかだとなかなか参加できなかったりするので、やっぱりMMよりは優先度が下がると思いますが。まあそれでも青には到達しておきたいと思います。
つい先日Psyhoさんによるヒューリスティック・ボットコンテストのための無料Tipsをまとめたところですが、こういうのを見ているとやはり自分自身でアウトプットを重ねてまとめるという作業は必須化のような気がします。まあ今の時点でもそれなりに自分用のドキュメントを作ってはいますが、どんどん公開していったほうが良いかもですね。
ではまた来年!
Psyhoさんによるヒューリスティック・ボットコンテストのための無料Tips
ある日、マラソン王者のPsyhoさんがつぶやきました。
要約すると、Let's make a silly experiment.
— Psyho (@FakePsyho) 2022年12月21日
For every like this post receives in the next 24 hours, I will post one tip for heuristic/bot programming contests.
I will start posting these as a thread in ~1h from now.
I could talk about those things for days, so bring it on!
これから24時間、1いいね毎にヒューリスティック/ボット プログラミングコンテストのヒントを投下します。
という話です。このまとめ記事を更新する時点で1000を超えるいいねがついていて、皆Psyhoさんのありがたいお言葉を楽しみにしています。というわけで、私が1つ残らず捕捉して順次日本語にしていきます。基本的にはDeepLとChatGPTで翻訳して、そこからさらにざっくりと私が適当にまとめました(意訳がちょっとあるのと、見出しや補足のために多少の追記があります)。まずは精度よりも速度重視でやっていきますので、翻訳に問題がある場合はご指摘いただけるとありがたいです。 英語を読むのが辛くなければ実際のツイートを見るのがベストですが、どうしても英語がツライという方はどうぞご利用ください。
- 一般的な話題(その1)
- 焼きなまし法(SA)について
- テストについて
- 一般的な話題(その2)
- #26: バージョン管理は悪
- #27: バージョン管理は悪だがテストを実行するときは別
- #28: コードを最適化する価値があるかどうか迷ったら、制限時間を延ばして実行してみる
- #29: 言語の選択 - C++は孤高の王者
- #30: 何よりもバグを取り除くことを優先すべき
- #31: 直感に反する結果が突然出たら、その度に調査をする
- #32: 解答コードは小さくまとめる
- #33: コンテスト参加後は必ずフォーラムを読むこと
- #34: 良い解法には時間がかかる
- #35: 実行 > アイデア
- #36: 問題文やテスターのコードを隅々まで読む
- #37: 何が自分のモチベーションになるかを見つける
- #38: 大して良くならない解法に時間を浪費しない
- #39: ツールで生産性が爆上がり
- #40: 優れた競争者はアイデアが尽きない
- 競プロ(アルゴ)的なお話
- 初心者向けアドバイス
- #46: プログラミングの初心者にはH/Bコンテストを勧めない
- #47: コンテストを見つけ、そのための時間を確保し、ベストを尽くそう
- #48: 出場しなくても、問題を読むのはアリ
- #49: コンテスト開始当初は(コンセプト的に)シンプルな解法の実験に集中すること
- #50: 可能性のあるアプローチを評価する良い方法は、良い答えで終わるために、どのようなステップを実行しなければならないかを考えてみること
- #51: 小さな漸進的な変更に集中する
- #52: コードの最適化は、悪い解法を素晴らしい解法に変えることができる
- #53: もしテストやゲームの結果に一貫性がないと感じたら、それはテストやゲームの数を増やせということ
- #54: Pythonをコンテストに使わない
- #55:自分を信じること。
- 最適化のお話
- #56: コードの最適化に理論的考察の必要なし
- #57: N次元の座標は1次元に統合する
- #58: メモリ割り当ては非常に遅い
- #59: 本当に必要なデータ構造は配列だけ
- #60: 剰余演算子は驚くほど遅い
- #61: できることはすべて事前に計算し、それらの値を配列に格納しておく
- #62: 大きな配列を扱う場合、可能であればできるだけ小さな変数型を使用する
- #63: Fast-Clearing Arrayを使う。
- #64: Fast-Clearing Arrayを拡張する
- #65: グラフには番兵を置く
- #66: 一般的に最も重要な高速化は、アルゴリズムを差分にすること
- #67: 時間の計測はコストがかかる(ことがよくある)
- #68: プルーニング/早期終了/単純化された計算を使用する
- #69: 非常に重いコードの最適化を行う場合は、ジャッジマシンをミラーリングする
- #70: SIMD/自動ベクトル化は超強力
- #71: [gcc]コンパイラのフラグ
- ボットコンテスト(コドゲ)について
- ここで一区切り
- この記事の作成者より
一般的な話題(その1)
#0: 無料のアドバイス
誰もが個性的で、いろんな背景を持っています。一人一人が異なるテーマで苦労しています。 すべてのアドバイスがあなたに当てはまるわけではありませんが、できるだけ一般的なものにするよう心掛け、状況に特化したものがある場合はその旨を述べるようにします。
#1: 1週間あれば、コンテスト中にあらゆる研究ができる
たとえ経験が浅くても、ひとつのコンテストに一所懸命取り組めば勝つチャンスはあります。これは何年も練習が必要な短期のプログラミングコンテストとは対照的です。
#2: 高度な数学は必要ない
シミュレーションのコードを書くという選択肢は常にあります。私が参加した約200のコンテストで、数学の知識があったために良い成績を収めた例は1つもありません。例外があるとすれば、ベイズの定理くらいですね。ちなみに私は微積分を知りません😅。
#3: ヒューリスティック(以下H)コンテストでは、ビームサーチと焼きなまし
グラフ理論、動的計画法、線形計画法、フロー問題などをきちんと経験しておくと便利な場合もあります。
#4: タッチタイピングは超重要
もしタッチタイピング(いわゆるブラインドタッチ)ができないなら、最優先すべきです。だいたい10時間から30時間くらいかかると思います。 タッチタイピングをすることで、コーディング中に他のことを考えることができるようになります。バグの数を減らし、プロトタイピングをスムーズにする、などなど。
#5: H(ヒューリスティック)コンテストとB(ボット)コンテスト、どちらが良い?
標準的なテクニックの違い以外に、主な違いは、Hコンテストでは迅速かつ正確なフィードバックが得られるのに対し、Bコンテストでは一般的により楽しいということです。 Hコンテストでは、より速いペースで学習することができます。
#6: コンテストを開催するのに最適なサイト
H: Topcoder (マラソン), AtCoder (AHC) B: CodinGame (今、コンテストが開催されています!) どのサイトも、良い問題、公平な評価システム、コンテスト後に解法について話し合うコミュニティが特徴です。 UIが荒いサイトもあるかもしれません;)
#7: [H]問題についてググるのは大体時間の無駄
良い問題デザイン(上記のサイト)とは、問題作成者が問題がユニークであることを確認したことを意味します。 ※まれに例外もあります。特定の部分問題でよく知られているものを研究するのはアリかもしれません。
#8: プロトタイピングのスピード
ほとんどの人にとって、最も制約の多いスキルはプロトタイピングのスピードです。 ある程度の経験を積めば、実装したいアイデアが常に何十個も出てくるようになります。それをいかに早く反復できるかということが、限界の要因です。速ければ速いほど、問題点を早く知ることができます。
#9: 1つのコンテストに集中する
早く上達するためには、中途半端に多くのコンテストに参加するのではなく、一つのコンテストに集中することが一番です。 基本的な解法ばかりやっていても、あまり身につきません。正しい学習期間は、壁にぶつかってどうしたらいいかわからなくなったときから始まります。自分を追い込まないと結果は出ません。
焼きなまし法(SA)について
#10: SAに代わる局所探索はすべて(ほとんど常に)ダメ
遺伝的アルゴリズム、タブーサーチ、蟻コロニー、などなど。これらは忘れてください。これらは効果が薄いだけでなく実装に時間がかかります。
#11: なぜSAなのか?
- 山登り法(HC)から始めて、2行追加でSAに変換することができる
- 高速な動的評価が可能
- 適切に調整すれば、他の手法よりも高いポテンシャルを発揮する(高速なので)
- 非常に高速なイテレーションが可能
#12: 標準的なSA
温度スケジュール: t = t_start * (t_final / t_start) ^ time_passed、time_passed は 0..1 の範囲
受理(最小値が良い場合): RNG() < exp((cur_result - new_result) / t)、RNG() は 0..1 を均一に返す
出発点としては、ほとんどの場合でこれが最も良いです。
#13: SAにおける温度管理は受理率がゆっくりと減少するようなものが良い
同じ受入率の値にずっと留まっていると、効果がありません。
#14: 局所最適解に陥りやすいときの対処法
- 非常に高い温度/加速度
- 複雑な遷移状態(※訳注:遷移状態を複雑にして解の変更を緻密にすることで、局所最適化から抜け出しやすくなる?)
- (まれに)キック(※訳注:解を強制的に変更する)
- (まれに)ソフトリスタート(解法は変えずに温度管理をやりなおす)
- (まれに)複数回実行
#15: 制約のために多くの状態が無効になる場合に行うこと
a) 初期重み0、最終重み∞の衝突回数に基づくスコアリング要素を追加する。 b) (可能であれば)部分的な解に対して高い温度で短いSAを何度も実行する。
#16: 評価が非常に高速の場合に行うこと
これはあなたの想像以上にずっとよく起こります。
#17: SAの全体的な優先順位
- 異なる遷移関数のプロトタイプを作る
- 評価関数を非常に高速にする(つまり動的にする)
- 適切な温度管理を見つける(通常3-4回実行するだけで十分)
- たくさんテストする
- 上記が終わってから、他のことに移る
#18: 常に最良結果を更新し、最終結果ではなく最良結果を返すようにする。
このミスを何度見たかわかりません。常に最良結果を更新することで、最終的な温度をより高くすることができます。
#19: SAがイマイチな場合
- 局所最適に陥りやすい: #14にヒントがあります。
- 単純な遷移と複雑な遷移が混在している: 各遷移に対して別々の受容関数を用意する。
- 遷移中に評価が非常に不安定になる場合: 運が悪かったとしか言いようがない さて、SAについてはもう十分でしょう。
コンテストは基本的に単純なフィードバックループです。 a) 何かをする b) 結果を得る c) 情報を抽出する
このうちのどれかを改善することで、より良くなることができます。しかし、最も軽視されているのは(b)の部分です。
テストについて
#20: テストはコンテストで最も軽視されている点である
テストは、フィードバックを得るための手段です。もしテストが遅ければ、進歩は非常に遅くなります。テストが不正確だと、正しい次のステップを見つけるのが非常に難しくなります。 Bでのテストは非常に難しく、ほとんど実行不可能なことが多いので、これは主にHに焦点を当てます。
#21: [H]ローカルのテスターを使う
もしあなたが評価のために仮のテストを使うだけなら、あなたは自分自身にとってすべてを非常に困難にしています。時間を節約するのではなく、無駄にしているのです。 (※訳注:ローカルでテストせずに提出してスコア確認するのは時間の無駄ですよ)
#22: [H]良いローカルテスターを使う
絶対に必要なのは、次の2つの機能です。 - マルチスレッド(複数のテストを別々のスレッドで実行する機能) - 相対スコアリング(これはtopcoderの標準機能です) もし自分で持っていないなら、私のものを使ってください: https://github.com/FakePsyho/mmtester
#23: テストの速度は制約になりやすい
あなたの解法がコンパクトで簡単に拡張できる場合、数秒で機能を追加/削除することができます。つまり、コンテストのある時点で、解法の異なるバージョンをテストすることが主なボトルネックになりそうなのだということです。
#24: 素早いテストのために外部VMを使用する
強力なマシンを持っていない場合は、AWS/GCP/Azureを使用して素早くテストすることができます。Linuxの知識があれば、1-2時間で習得できます。スポットを使えば、5ドルであなたのノートパソコンと同等のものを1週間稼働させることができます。
#25: テストをできるだけ頻繁に実行する
コンテストでは、自分でテストができるようにテスターが用意されています。 テストを行えば、あなたがどこかでミスをしたのかがよくわかりますし、改良点についてのフィードバックも得られます。
一般的な話題(その2)
#26: バージョン管理は悪
あなたはgitの使い方にとても慣れていて、それでスピードが落ちることはないと感じているかもしれません。そしてそれは真実かもしれません。とはいえ、もしそれが自分にとって便利だと感じているのなら、あなたはプロトタイピングが下手なのです。プロトタイピングのスキルを見直しましょう。
#27: バージョン管理は悪だがテストを実行するときは別
テストを実行するときは現在のソースファイルを保存しておくと便利です。これは、予期せぬ結果が出たときのサニティチェック(※訳注: ある状態や結果が正しいかどうかを確認する)として機能することが多いです。テスト時にソースファイルを保存する短い.sh/.batスクリプトを作るだけでよいでしょう。
#28: コードを最適化する価値があるかどうか迷ったら、制限時間を延ばして実行してみる
これは非常によく使われるシンプルなテクニックです。潜在的な利益が非常に低い場合は、コードを最適化しないようにしましょう。
#29: 言語の選択 - C++は孤高の王者
マクロはC++の問題の多くを解決することができますが、あなたが何をしているかを知っていれば、C++から他の言語よりもはるかに多くのものを絞り出すことができます。 *私はRustの経験がない+非常に複雑なトピックなので、あまり真に受けないでくださいね。
#30: 何よりもバグを取り除くことを優先すべき
バグがある場合、その解法はあなたが思うようには機能しません。これは、テストを実行するたびに、間違った結果を得ることを意味します。問題に対する直感が正しく育たなくなるのです。 とても重要なことです。
#31: 直感に反する結果が突然出たら、その度に調査をする
バグがあるのか(上記参照)、直感が狂っているのか、どちらかです。後者の場合は、これを学習経験として扱い、なぜ間違っていたのかを突き止める必要があります。
#32: 解答コードは小さくまとめる
コードが多くなると - バグが増える - コードの内容を全部覚えるのは、精神的にもっと大変です。 - (通常)依存関係が多くなる -> リファクタリングのコストがかかる 上位の多くは、400-1000行程度のコードです。
#33: コンテスト参加後は必ずフォーラムを読むこと
これまで述べてきたすべてのプラットフォームにおいて、(ほぼ)すべてのトップクラスの競争相手が、コンテストが終了した後に自分の解法を説明しています。コンテストに参加した後、他の人が何をしたかを読まないのは、信じられないほど無駄な機会です。 では、なぜそのようなコンテストで常に優秀な人がいる一方で、常に苦戦している人がいるのか、その理由を説明しましょう。
#34: 良い解法には時間がかかる
まず当たり前のことですが、良い解法を開発するには時間がかかります。 魔法のようなテクニックや回避策はありません。でも、時間が経てば速くなりますよ。
#35: 実行 > アイデア
なぜ、多くの異なるアプローチが上位にあるにもかかわらず、どれも同じようなスコアなのか、不思議に思うかもしれません。このような場合、「完璧なアイデア」を持つことよりも、「うまく実行すること」が重要です。
#36: 問題文やテスターのコードを隅々まで読む
問題文の細かい部分を思い出せるようになるまで、問題文を読み直しましょう。テスターのコードも同様に読みましょう。 最初に読んだときには見逃していたような小さな詳細がよくあります。特に、非自明な論理を含む場合は、提供されたコードも読んでください。
#37: 何が自分のモチベーションになるかを見つける
多くの競技者にとっての最大の原動力は、自己研鑽の喜びです。HでもBでも、未来の自分が過去の自分より良くなろうとする孤独なゲームであることがほとんどです。他の競争相手をベンチマークとして扱い、自分の目標とはしないことです。
#38: 大して良くならない解法に時間を浪費しない
現在の解法が良い結果を出せないことがわかっているなら、それを最大限良くしようとしても意味がありません。 リーダーボードの頂点に立つ最も簡単な方法は、高い目標を掲げて失敗することです。
#39: ツールで生産性が爆上がり
Hの場合は主にローカルテスター。Bの場合はローカルリーグ方式です(信頼性は低いですが)。私の試算では、ローカルテスター(リンク先)を改良した後、コンテストに費やす時間が30~40%程度減りました。
#40: 優れた競争者はアイデアが尽きない
テストを実行したり、ビジュアライザー(H)/ゲーム(B)を見たりすることで、より多くのインスピレーションを得ることができます。解法に取り組むことで、アイデアを得ることができるのです。最初のうちは、どんなに優秀な人でも、何がベストな解法なのか、まったくわからないものです。
競プロ(アルゴ)的なお話
また切り替わる。CodeForcesからたくさんの人が参加してくれたので(マイクありがとう😁)、古典的な競技プログラミング(CP)とH/Bコンテストの違いについて話してみようか。 ちなみに、今はもうクラシックCPはやっていませんが、topcoderで4位になった時期もありました。
#41: CPとH/Bコンテストは全く違うスキルが必要
CPは短距離走で、非常識な集中力と豊富な知識が必要です。 H/Bはマラソンで、長期的な計画と創造的思考・問題解決が主体です。
#42: CPの場合「相手」は問題設定者であり、H/Bでは(主にH)、相手は過去の自分である
H/Bでは問題解決に終わりはなく、解決は継続的なプロセスです。コーディングセッションの間に自分の生活を合わせなければならない。問題の切り替えが非常に難しいのです。
#43: CPでは最悪のケース、H/Bでは平均的なケースを気にする
これにより、完全に新しいクラスの技術が開かれます: - ランダム化アルゴリズム - 特殊なケースを素早く処理するための様々なバージョン - プルーニング(早期終了) (※訳注: プルーニングは計算時間やリソースを削減するために処理を途中でやめることで、探索アルゴリズムだと枝刈りのようなものだと思ってください)
#44: CPの経験があると、H/Bコンテストの基礎が固まる
CPのアルゴリズム知識はある程度しか役に立ちませんが、非常に比較的短時間で繰り返しコードを書くため、プログラミング言語の練習やバグのないコードの書き方を身に付けるにはとても効果的です。
#45: CPは就職に有利、H/Bは仕事ができるようになる😁
多くの企業が採用活動でプログラミングパズルを使用しますが、CPはそれ以上に大して役に立ちません。H/Bコンテストは、AI企業に入社するとよく遭遇する小規模な研究に似ています。
初心者向けアドバイス
では、初心者の方へのアドバイスです。
#46: プログラミングの初心者にはH/Bコンテストを勧めない
もしあなたがプログラミングの初心者なら、H/Bコンテストはお勧めしません。 まずCPに挑戦し、言語のシンタックスを学び、BFS/DFSや1次元DPなどの簡単なアルゴリズムを学びましょう。基本的なことを素早く理解するためには、より速いフィードバックサイクルが必要です。
#47: コンテストを見つけ、そのための時間を確保し、ベストを尽くそう
おそらく失敗するでしょうが、それでいいのです。失敗することは学ぶことであり、勝つことは何も教えてくれません。自分がうまくいかなかったと思う理由をすべて書き留めておいてください。自分が苦労しているところを見つけるのです。
#48: 出場しなくても、問題を読むのはアリ
以前見たことのあるような新しいコンテストを見かけたらフォーラムを全部読んで、何か応用できそうなことがないか見てみましょう。 少ない経験で良い成績を残すには、圧倒的に簡単な方法です。
#49: コンテスト開始当初は(コンセプト的に)シンプルな解法の実験に集中すること
あなたの目標は、問題に対する直感を養うことであって、手っ取り早く得点を稼ぐことではありません。アドレナリンが出るのは良いことですが、長期的には何の役にも立ちません。
#50: 可能性のあるアプローチを評価する良い方法は、良い答えで終わるために、どのようなステップを実行しなければならないかを考えてみること
もし、それが不可能であったり、非常にあり得ないと思うのであれば、おそらくそれは良いアプローチではないでしょう。
#51: 小さな漸進的な変更に集中する
解法を書き換えることは避けましょう。 小さな変更=速いフィードバックサイクル、少ないバグ、より良いモチベーション。ちなみに、私は自分の解法を書き換えたことはありませんし、テストせずに10~15分以上経過することはほとんどありません。
#52: コードの最適化は、悪い解法を素晴らしい解法に変えることができる
ほとんどの反復的アプローチ(SAなど)では、そのアプローチが良い結果を生むまでに、ある程度の重要な反復回数/ステップを必要とします。コードの最適化によって、全く新しい可能性が開けることもあるのです。
#53: もしテストやゲームの結果に一貫性がないと感じたら、それはテストやゲームの数を増やせということ
解法が改善される一方で、テストの精度を高めるために、より多くのテストが必要になります。1回の実行で 2-5K テストを使用することは珍しくありません。
#54: Pythonをコンテストに使わない
Pythonはある用途には最適ですが、通常の操作ではおよそ100倍も遅くなります。妥当な速度を得るためには、コーディングやアルゴリズムで非常に創造的になる必要があり、それはあなたのコードがずっと複雑になることを意味します。そこまでする必要はありません。
#55:自分を信じること。
自分はうまくいかない、手が届かない、と盲目的に思い込んでしまうと、モチベーションを維持するのはとても難しいです。私は、考え方を変えただけで、突然良いパフォーマンスを発揮する人にたくさん会いました。
最適化のお話
さて、次はコードの最適化に関する一般的なテクニックを紹介します。
#56: コードの最適化に理論的考察の必要なし
ターゲットマシーン上でコードを実行し、それを測定しましょう。 コンパイラのバージョン、OS、プロセッサの違いは大きな影響を与えます。
#57: N次元の座標は1次元に統合する
これは非常によくあるテクニックです。2次元のグリッドがあり、その上でBFSを実行するとします。(行, 列)を使う代わりに、それらを1つの値にマージします。メモリフットプリント(※訳注:メモリ使用量と考えてください)、演算数、コード自体を減らすことができ、通常は10-30%高速化されます。
#58: メモリ割り当ては非常に遅い
メモリプールの経験(※訳注:自分でメモリの割り当てをやり繰りする経験と思ってください)がない限り、一般に、すべての配列を一度だけ割り当てるようにしたいものです。時間計算量と空間計算量がO(N)の関数では、呼び出すたびにメモリを再割り当てすると、最大で10-50倍の速度になることがあります。
#59: 本当に必要なデータ構造は配列だけ
本当に必要なデータ構造は配列だけです。すべてのデータを単純な配列に置き換えることができないのは非常に稀です。 とはいえ、データ構造の最適化は複雑さを増す可能性があるので、時期尚早と考えることもできます。
#60: 剰余演算子は驚くほど遅い
正直なところ、理由はわかりません。でも、そういうものなんです。 次のように書き替える、かなり高速になることが多いです。
x = (x + y) % m
を
x = x + y x -= x >= m ? m : 0 (y < m, y > 0, m > 0 と仮定して)
の方が速い場合が多いです。 (※訳注: typo修正済み)
#61: できることはすべて事前に計算し、それらの値を配列に格納しておく
常に良いというわけではありませんが、いくつかの演算は思ったより遅いかもしれません。例えば、"x ^ y"を事前に計算することは、その場で計算するよりもかなり速い場合があります。 (※訳注: これはxのy場を意味しています)
#62: 大きな配列を扱う場合、可能であればできるだけ小さな変数型を使用する
メモリコピー/クリアはバイト数だけを考慮します。これにより全体的なキャッシュ効率も改善します。単一の変数に対しては行わないでください。
#63: Fast-Clearing Arrayを使う。
3つの異なる操作を必要とするboolean配列をイメージしてください:
set(pos, value) check(pos) clear() - 配列全体をクリアする
ナイーブな実装ではO(1)+O(1)+O(N)ですが、カウンター(clear -> counter++)を持つint配列を使用することで、O(1)+O(1)+O(1)にすることができます。 (※訳注: tomerunさんのブログが参考になります)
#64: Fast-Clearing Arrayを拡張する
- クリアするたびにカウンタがxずつ増えるなら、0..x-1に値を格納できる。
- 衝突が許容されるなら、多くの場合、これはセット/マップを置き換えることができます。
#65: グラフには番兵を置く
グラフ内に特別なガード/境界を追加することで、経路探索中の操作数を削減できます。 例えば2DグリッドでBFSを実行する場合、境界条件のチェック(グリッドの外へのステップ)を避けるために、すべての方向に1ずつグリッドを拡張するとよいでしょう。
#66: 一般的に最も重要な高速化は、アルゴリズムを差分にすること
例えば、TSP(Traveling Salesman Problem)にSAを適用して、都市をパス上の別の地点に移動させる場合、Δにしか関心がないので、evalはO(1)であるべきです。
(※訳注: Δは変化量、差分という言葉は時間計算量が定数時間であると読んでください。)
(※訳注2: 当初は「差分」と書かれている部分を「動的」としていましたが、動的ではなく差分と解釈した方が良いのではとtoast-usさんからご指摘いただきました。確かに、ある状態を計算する場合や盤面の評価関数を計算する場合、前の状態を利用して差分計算するのは高速化にかなり良い影響を与えるという文脈だと思うので、それが良さそうです。)
#67: 時間の計測はコストがかかる(ことがよくある)
一番早いのは rdtscを呼び出す方法ですが、サイトによっては別の方法で時間を計測しているところもあります。c++でよく使われるgettimeofday()はシステムコールで、 プラットフォームによっては非常にコストがかかります。1Kコールで1秒以上かかったこともありました。
#68: プルーニング/早期終了/単純化された計算を使用する
これはあまり起こらないことですが、単純に計算をスキップする場合があります。これは主に評価関数で発生し、いくつかの遷移でスコアが完全に壊れてしまうので、すぐにわかります。 (※訳注: ちょっとわかりにくいですが、「評価関数において、ある遷移がスコアを完全に壊してしまうような場合、つまりスコアが良くなる見込みが全くないとわかった場合、その遷移を完全に打ち切る(枝刈りする)と良いですよ」という意味かと思います。)
#69: 非常に重いコードの最適化を行う場合は、ジャッジマシンをミラーリングする
gccの正確なバージョンを持っていることが一番重要です。 とはいえ、私は一般的に5%未満のスピードアップを目指す程度ならお勧めしません。パラメータの最適化の方がはるかに簡単です。
#70: SIMD/自動ベクトル化は超強力
私は最近これを使うことはありませんが、それでも強力なツールです。SSE/AVX命令セットを使うのは、ミニパズルを解いているような気分です。最高のコンパイラを上回るのは簡単で、重要な場所で2-20倍のスピードアップが可能です。
#71: [gcc]コンパイラのフラグ
"#pragma GCC optimize (...)"でコンパイラのフラグを(ほとんど)オーバーライドできるようになっています。 私は"Ofast,omit-frame-pointer,inline,unroll-all-loops"を使っています。理論上"omit-frame-pointer"は"-O1"に含まれますが、こちらの方が速かったです🤷。コンパイラのフラグでHC(山登り法)ができる😅。
(※訳注: 「inline、-O3、-ffast-math、-funroll-loops、... 他の便利なフラグはありますか?という質問に対してのツイートです」)
ボットコンテスト(コドゲ)について
ボットコンテストに特化した話をあまりしてきませんでしたので、ここからはそのお話をしましょう。 Bコンテストは形式も問題の内容もさまざまです。ここではCodinGame(コドゲ)に焦点を当てます。コドゲは頻繁にコンテストを開催する唯一のサイトです。
#72: ボットゲームの新しい概念
ボットゲームには新しい概念があります。それはメタゲームです。最良の戦略は、他のプレイヤーが採用する戦略によって大きく変わります。これは特に、不完全情報のあるゲームで問題が発生しやすいです。自分の解法をまともに評価することは忘れてください。
#73: 勝つか負けるのみ
各テストは本質的には、二者対戦ゲームであり、勝ちか負けかという2値の結果になります。どれだけ大きな優位/劣勢があっても、勝ちか負けかにしか過ぎません。自分の解法をまともに評価することは忘れてください。
#74: ローカルテスト
ローカルでうまくテストを実施できるようにするには、リーダーボード上のボットに代表される様々なアプローチを持つ必要があります。 解法をまともに評価することは忘れてください。 (※訳注: 自分のボットをテストするには、他のさまざまなボットと対戦するとよいといういみだと思います)
#75: フィードバックは重要
#20を覚えていますか?コンテストはフィードバックのループです。自分の解法を効果的に評価できない場合、直感力を高めることは困難です。 ボットコンテストでは、ノイズの多いフィードバックを受け、次のステップについて非常に大胆な推測をする必要があります。
#76: ボットコンテストは時間投資が大きい
ボットコンテストは、ヒューリスティックコンテストよりはるかに大きな時間投資を必要とします。 - フィードバック機構が非常に弱い - 常に進化するメタゲーム - すべてのリプレイにアクセスできるため、誰もがあなたのボットのプレイを知ることができる(そして、それに対抗することができる) - (しばしば)より複雑なルール
#77: 楽しいけれども初心者向けではない
ボットコンテストはインタラクティブなため、同じようなヒューリスティックコンテストよりもずっと楽しいものになる傾向があります。しかし、私は一般的にボットコンテストを初心者のための良い学習プラットフォームとして勧めません。フィードバックループが効果的でないため、自分の行動と結果を関連付けることが難しくなります。
#78: HスキルはBでも役立つ
Hで得たスキルや知恵のほとんどは、Bコンテストにも適用できます。 プロトタイピング。良いワークフロー。コードの最適化。多くのアルゴリズムとテクニックが適用できます(ビームサーチも使えます)。
#79: 2種類のテクニックのタイプ
多くのテクニックは2つのタイプに分類されます。1つは複雑な状態評価(別名ヒューリスティック)関数、もう1つは検索(ビームサーチ、ロールアウト、MCTS)です。 どちらが有効かは問題によって大きく異なりますが、成功するためには両方をマスターする必要があります。状態評価にニューラルネットが使えれば最強です。
#80: ノイズを無視する
評価は非常にノイズが多いので、それを完全に無視して、うまくいくと思われる解法に集中するのが良い場合があります。 検索ベースの解法は、メタゲームにあまり依存しない傾向があります。また、ローカルリーグのシステムを開発し、状態評価の調整を自動的に行うのもよいでしょう。
ボットコンテスト用のツール
これはヒントではありませんが、私は自動マッチメイキングを行う簡単なローカルリーグシステムに取り組んできました。mmtesterと似たようなものですが、ボットコンテストのためのツールです。 近い将来、PyPIパッケージとして公開できればと思っています。
#81: [コドゲ限定]持ち時間の使い方
通常、最初のターンの制限時間は1秒ですが、次のターンでは50ミリ秒になります。相手の行動が限られている場合は、最初のターンで2-3ターン先を「考える」ために使うのは非常に有効です。
#82:
現在のメタゲームを追いかけ、トッププレイヤーを真似ることで順位が良くなるかもしれませんが、長期的にはあまり多くの学びにはなりません。 もしあなたの目標が自分自身のレベルアップなら、そういったことを避けてみてください。
ここで一区切り
お話ししたいことは一通り触れたと思います。もちろんTwitterのスレッド上なので、共有すべき知識や知恵が大量にあることに比べればとても浅いものですが。 あとはQ&Aとまとめのために残しておこうと思う。 おやすみなさい💤。
この記事の作成者より
この先はQ&Aがいくらか続くと思いますが、何か目についたものがあれば追記しておきます。内容的な修正と見やすくする作業は続けます。
競プロ日記010: MM142に参加しました
TopCoderマラソンマッチ(MM142)に参加しました.最終結果は19位でした.
問題の概要

プレゼントをエルフがグリッド外まで持ち出すことができれば,盗んだとみなされます(つまり持っているだけではダメです).すべてのプレゼントを盗むことに成功すると,N×Nターン経っていなくてもプログラムは終了します.プログラムが終了したとき,持ち出したプレゼント数×100と,終了までにAIが使用したお金の合計額を加えたものがスコアになります.たとえばプレゼントを3個盗み出し,その間AIが50のお金を使ったとすると,スコアは350になります.
やったこと
最初の解答
おそらく多くの人がやったであろう,
- プレゼントまでの最短経路を通ってプレゼンを取る
- プレゼントからグリッド外への最短経路を通って脱出する
- プレゼントまでの経路が見つからない場合は適当な箱に対して同じような処理を行う
といったものでした.当然プレゼントまで進む途中に箱を置かれてしまうので,プレゼントを取れずに箱ばっかり取る事になります.それでもCが大きくグリッドが大きいものであればそれなりにプレゼントを取ってくることができるので,これだけでも70点くらいは取れそうな感じです.経路の計算が間違ってて最短経路じゃない場合,AIが余計に箱を設置することになってスコアが少しだけ高くなったりすることもありましたが,そういうので得点が上がってもあまり嬉しくないです.
2番目以降の解答
2番目以降の提出では,プレゼントまでの経路中に箱が置いてある場合への対処を主に行いました.








やりきれなかったこと
私の解答では,上手くいった場合に上記のような動作をしてくれますが,実際のところはいろいろと不具合があって,エルフが閉じ込められたりすることも結構ありました.対処としては,脱出したいエルフの逃走経路を確保するために別のエルフを派遣することです.これも上手くいったりいかなかったりなので,しっかり修正して提出したかったですが間に合いませんでした.あとは逃走経路に他のエルフが立ち入ってしまってデッドロック状態になる場合もあって,その辺の対処も不完全でした.この辺りがもう少しスッキリ書けていれば,もう1~2点上がるかなーと思っています.
それから,この問題では5種類のAIがランダムに選ばれるので,上位に入ろうとするならAIの特定と,それらに対して最適な行動ルールを設計すべきです.これには各AIの特性を見極めるとかソースコードをちゃんと読むなりしないと行けないので,とても大変そうです.考察力とか実装力が高まればその段階に進めると思いますが,今のところは難しいです.
ハイレベルな解法
simanさんのブログやValGrowthさんのブログにわかりやすい解説がありますので是非ご参考に!
日記
以下,メモしていた日記を簡単にまとめておきました.あまり得るものはないです.
12/8(Thu)
午前2時開始と思い込んでいましたが,3時からでした.3時になると同時に登録して,いつも通りサンプルコードとテスターのダウンロードを済ませました.その後「あーこれ系かー」と思いつつもよくわからず入眠.お昼にサンプルを動かそうとしてけれどもテスターが動かなくて困った.どうもファイルパスの問題っぽいのでフォーラムに質問したら修正版を用意してくれた.これで戦える!という感じだけど今日はこれで終わりっぽい.疲れた.
12/9(Fri)
方針を決める.とりあえずプレゼントを狙えば良い気がするので,プレゼントからグリッド外への最短ルートを調べることにする.しかしルートの途中に箱があると通れないので,箱を処理する部隊が必要.箱を持っていると他の箱を乗り越えられないため,ルートの歩数分だけ人数が必要になる.まあその辺はあとで考えるとして,各プレゼントを起点とした枠外へのルートを取得する部分から書き始めることにした.
12/10(Sat)
実装が結構大変な気がするので,まずはシンプルに箱とかプレゼントを拾ってくるコードを書くことにした.基本的なコードは書けたけど完成はせず.明日に持ち越し….
12/11(Sun)
いろいろと勘違いに気付く.
- 箱やプレゼントがあるマスに移動すると自動的にそれを拾ってしまう(拾うかどうかを選択できると思ってた)
- ターン毎の出力に改行を入れちゃダメ
修正したものをひとまず提出して70点くらい.まあそんなもんかな.seed1で1つもプレゼントが拾えてないので,まずはこれをどうにかする必要がある.プレゼントまであと1歩のところまで来ると目の前に箱が置かれるので,その時点でもう1人エルフを連れてくる必要がある.
12/12(Mon)
プレゼント毎にチームを作れば良いんじゃないかとか考えすぎて無駄なクラスを設計しまくった結果酷いコードが出来上がった.あまりに出来が悪すぎて最初の解答とさほど点が変わらずコード量だけが膨れ上がった.
12/13(Tue)
膨れ上がったコードにいろいろと機能を追加する.どんどん酷くなる.泣きそう😢
12/14(Wed)
書いたコードを全部捨てることを決断する.最低限やることをルールベースで書き直す.最終提出2時47分で前回に引き続いてまたギリギリ.大変疲れた.
感想
こうやって振り返るとかなり無駄な作業が多かったので,時間が無かったのではなく時間の使い方がとても悪かったということがわかりました.今回はテスターの不具合で早々に精神を削られたのでモチベーションの維持が結構大変でした.こういうゲームっぽいお題は結構好きな系統なんですが,その割には問題へのアプローチ方法が整理されておらず試行錯誤が多すぎるように感じたので,無駄な行動を減らすためにしっかり復習せねばと思いました.



